El passat 14 de març va ser el Dia Internacional de les Matemàtiques i a Ciència Oberta som tan despistats que no ho vam celebrar. Però, per què necessitem un dia dedicat a les matemàtiques? La resposta és evident! Perquè són magnífiques. I, així i tot, molta gent les odia. Avui, farem aquest article en honor al Dia Internacional de les Matemàtiques i, a partir de dos exemples, us intentarem convèncer que són molt més interessants del que us penseu!

Com es fan les matemàtiques?

Ja en vam parlar en detall a un altre article. Partint d’unes bases que considerem certes –els axiomes– es va construint el món matemàtic a base de demostracions completament rigoroses. A part d’això, no hi ha cap altra limitació! Godfrey Harold Hardy, a la seva “Apologia d’un matemàtic”, diu que “si la música és l’art d’ajuntar notes, les matemàtiques són l’art d’ajuntar idees”. Al món matemàtic no hi ha límits, només la teva pròpia creativitat.

Avui intentarem fer una d’aquestes demostracions tan elegants. Hem parlat molt dels nombres primers, aquells que només es poden dividir entre ells i entre 1 sense que el resultat doni decimal –la divisió té residu zero. De fet, són fonamentals en criptografia.

Vam veure també que els nombres primers són els àtoms de la resta de nombres:  qualsevol nombre es pot descompondre en producte de primers. Així, 35=5×7 o 143=13×11. A més a més, sabem que, a diferència dels àtoms, de nombres primers n’hi ha infinits. Com podem demostrar aquest fet?

Hi ha infinits primers

Tenim el 2, el 3, el 5, 7, 11, 13, 17, 19, 23, 29… res ens indica que arribi un que sigui l’últim, però això no passa. Cal demostrar-ho. Haurem de pensar alguna estratègia de pensament lateral: no podem comprovar-los tots! Farem el següent: suposarem que n’hi ha un nombre finit i mirarem si arribem a una conclusió absurda. Això és el que va fer Euclides farà milers d’anys!

Si tenim un nombre finit de nombres primers, els podem escriure per ordre en una llista: 2, 3,…, P; on P és l’últim nombre primer –ja que hem suposat que s’acaben. La idea és trobar un nombre primer que no estigui a la llista. El que fem és multiplicar-los tots i sumar-hi 1. Diguem-li Q a aquest nou nombre:

    \[Q=(2 \cdot 3 \cdot \dots \cdot P)+1\]

Clarament no podem dividir Q per cap primer de la nostra llista, ja que el resultat tindrà com a residu 1 –pel nombre 1 que hem sumat! A més, Q no està a la llista, i per tant no és primer.

Però no havíem dit que qualsevol nombre es podia descompondre en una multiplicació de primers? No hem trobat cap primer que divideixi Q i en conseqüència cap dels nostres primers pot  formar part dels àtoms que el constitueixen. Hi ha d’haver algun primer que ens falti a la llista que divideixi Q. És a dir, hem arribat a un resultat que contradiu la nostra hipòtesi! No serveix de res afegir un element a la llista: podrem tornar a utilitzar el mateix argument i trobar, de nou, un primer que hi falti. Això només pot voler dir que hi ha infinits primers!

Hem vist un dels maons sobre els quals es construeix l’edifici matemàtic. Bé, hem fet una mica de trampa, perquè no hem demostrat que qualsevol nombre es descompon en un producte de primers. Aquest maó s’hauria d’haver col·locat prèviament. Però així és com es va fent aquesta ciència. Aquesta demostració és increïble: usant arguments molt senzills hem posat un peu més a comprendre què vol dir infinit, mentre que nosaltres som completament finits! En aquests arguments i resultats és on molta gent veu la bellesa de les matemàtiques.

Però les matemàtiques també són molt útils!

I d’això n’hem vist munts d’exemples a Ciència Oberta. Avui us en porto un de curiós. Es coneix com la Llei de Benford, i va ser descoberta per primer cop l’any 1881 per l’astrònom americà Simon Newcomb.

Newcomb es va adonar que als llibres de taules de logaritmes –que s’usaven quan no hi havia ordinadors– les primeres pàgines estaven més gastades. Semblava que la gent consultava més els logaritmes de números que començaven per 1 o 2.

Va ser Benford qui va descobrir que moltes coses observades a la natura, com ara la llargada d’un riu, la població dels països o fins i tot dades econòmiques no estaven uniformement distribuïdes, sinó que tenien més probabilitat d’aparèixer els valors amb la 1a xifra més baixa. En aquest gràfic veiem que els nombres que tenen un 1 com a primera xifra són més probables que apareguin que els de 2, i aquests més que els de 3, etc. Benford va comprovar aquest fet experimentalment.

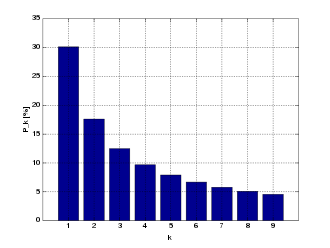
1. Distribució del primer dígit segons la llei de Benford

Perquè passa?

Hi ha diverses explicacions d’aquest fet, però és fàcil veure-ho en el cas de les dades bancàries. Si partim d’un capital de 100 €, la primera xifra és un 1. Per canviar aquesta xifra, hem de sumar 100 € al nostre capital. Aquest canvi suposa el 100% del nostre capital –100 € respecte a els 100 € que tenim–, però aquest percentatge es redueix a mesura que augmenta la primera xifra. Així, de 200 € a 300 €, l’augment és del 50%, i anar fent. Per aquest motiu, aquesta llei es mostra en dades que canvien molt d’escala, com la població en diferents països. En dades que no ho fan, com l’alçada d’una persona, no la veiem.

Aquesta llei, que va ser considerada una curiositat, ha ajudat a resoldre crims d’evasió fiscal: si has de blanquejar diners ingressant-los en un compte bancari, evidentment no faràs 1000 transferències de 100 €. Seria molt sospitós! Intentaràs fer transaccions entre 0 i 100 € aleatòriament. Això no obstant, les teves dades bancàries no seguiran la llei de Benford i algun inspector d’Hisenda competent se’n podria adonar!

Ja per acabar

A Ciència Oberta hem vist molts més exemples de la bellesa de les matemàtiques: amb arguments senzills podem arribar a comprendre coses increïbles, com per exemple l’infinit o com dibuixar només utilitzant cercles.  Aquest és un dels principals motius pels quals hi ha gent que li agrada tant estudiar-les i des de Ciència Oberta esperem que vosaltres també n’hàgiu gaudit una estona.

Per saber-ne més

Wikipedia – Benford’s law

Viquipèdia – Godfrey Harold Hardy

Viquipèdia – Teorema d’Euclides

Fotografies: 1 extreta de WikipediaCommons.