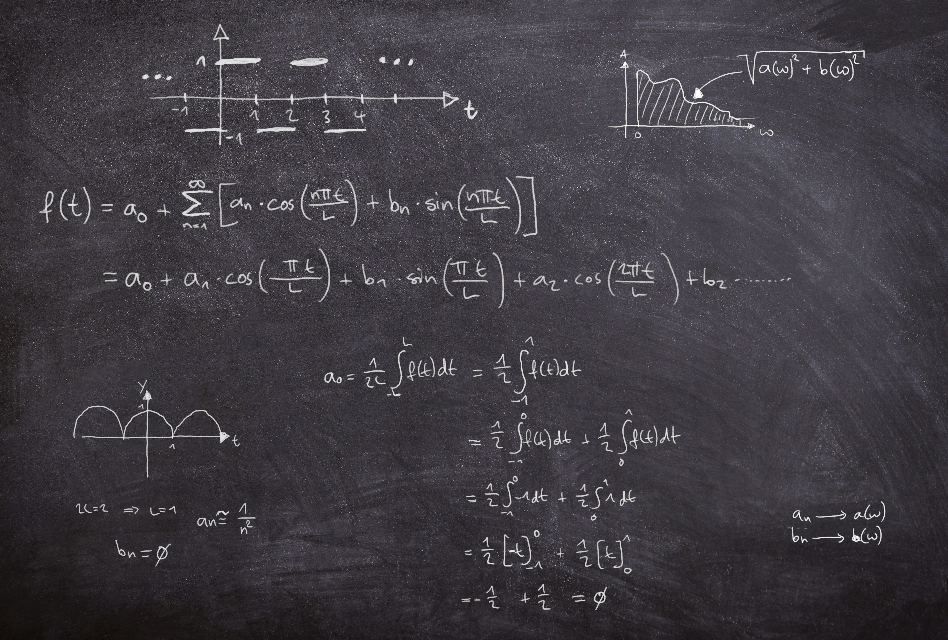Amb només petits rellotges, amb punts que girin a una velocitat constant, unint extrem amb extrem, podem crear qualsevol dibuix tancat que se’ns acudeixi!

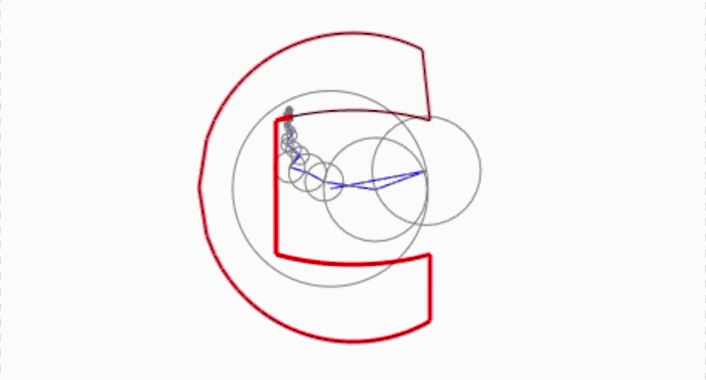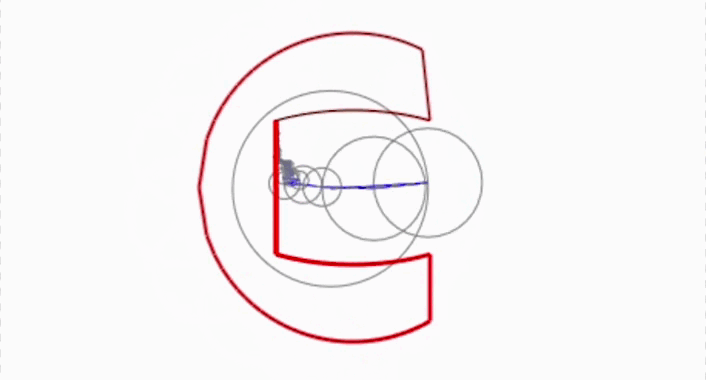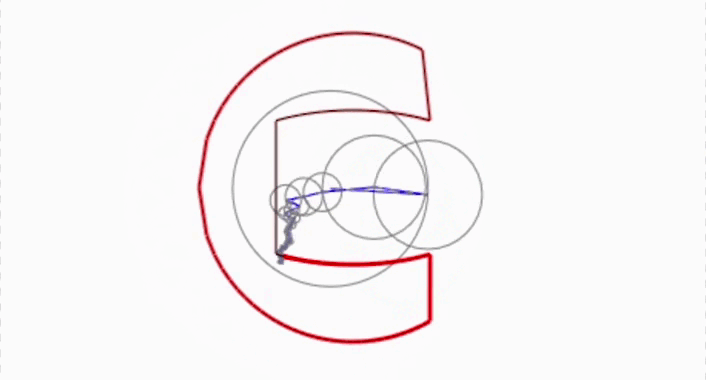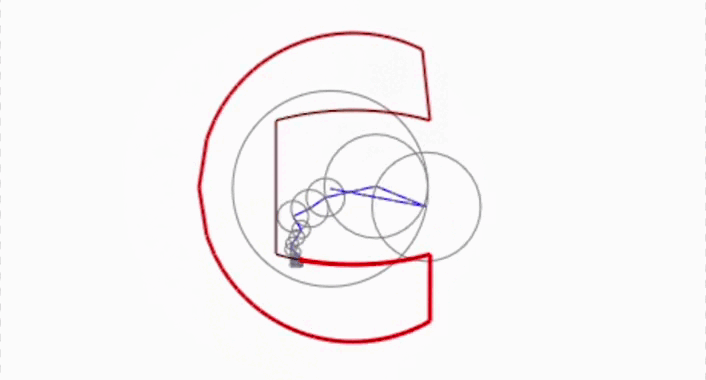
Aquest és un resultat matemàtic potentíssim que va desenvolupar el matemàtic francès Joseph Fourier quan intentava resoldre un problema de física. Usant coses molt senzilles: el moviment d’uns punts a velocitat constant en un cercle, podem descriure qualsevol dibuix tan complicat com vulguem!

La barra calenta

Fourier intentava resoldre el problema següent:

Tens una barra amb una temperatura diferent al llarg d’aquesta ーper exemple la meitat de la dreta està a 30ºC i la de l’esquerra a 10ºCー i vols saber, passat un cert temps, a quina temperatura estarà cada punt de la barra

Aquest problema es pot resoldre fàcilment si la temperatura inicial té una distribució molt concreta: en forma de la funció sinus ーque després en parlarem. Però què passa si aquesta no és la funció inicial? Necessitem un mètode per descompondre la temperatura inicial en una suma de sinus!

Func… què?

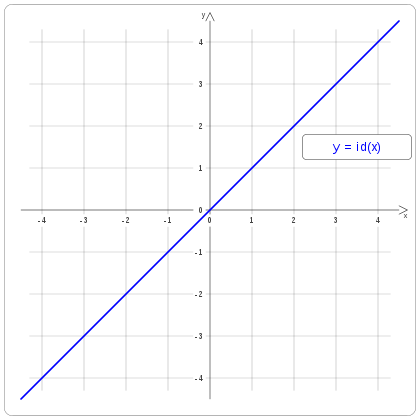
Ja hem parlat altres vegades de funcions matemàtiques. Una funció no és més que una màquina que, en donar-li un número, en retorna un altre. Un exemple molt senzill és la funció identitat, que en donar-li un número retorna el mateix. Usem el llenguatge matemàtic per expressar aquesta idea de forma sintètica. Així, si a la funció li diem f i al número qualsevol que li posem x, podem escriure que la funció identitat és

    \[f(x)=x\]

Per exemple, en el zero, la funció val zero, perquè és la identitat i ens retorna el mateix valor. Amb aquest llenguatge, si substituïm x per 0, tenim que f(0) = 0.

A continuació ho representem en un gràfic: a l’eix horitzontal hi posem el valor de x i al vertical el que pren la funció quan li donem aquest valor x. Així, com que en el zero la funció val zero, posem un punt blau allà i així per cada punt. 

1. Gràfic de la funció f(x)=x o identitat

Però aquestes funcions no ens serveixen en el cas de Fourier. Volem funcions periòdiques. És a dir, aquelles que es van repetint passat un període. Aquí tenim a la part central la funció identitat, i llavors la mateixa funció copiada i enganxada per a convertir-la en periòdica:

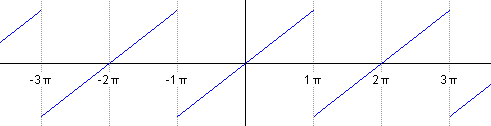
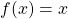2. Gràfic de la funció f(x)=x perioditzada amb període 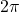2\pi o “funció dents de serra”

I què és un sinus? És una funció d’angle: surt en fer girar un punt en un cercle de radi 1. Si mirem com el punt puja i baixa només, tindrem els valors de la funció sinus. És la típica funció de les onades. Aquí podem veure com si dibuixem el que fa el punt en l’eix vertical trobem la funció sinus:

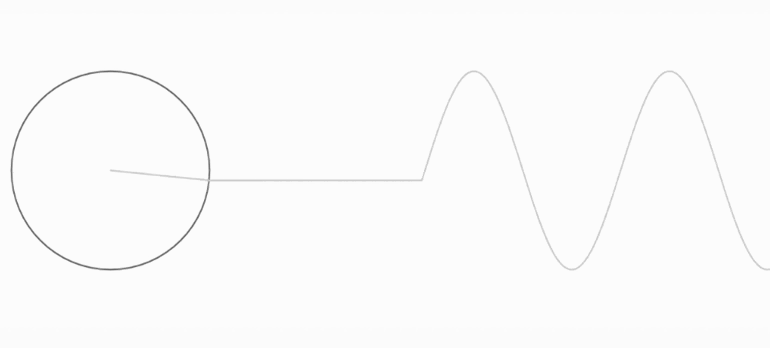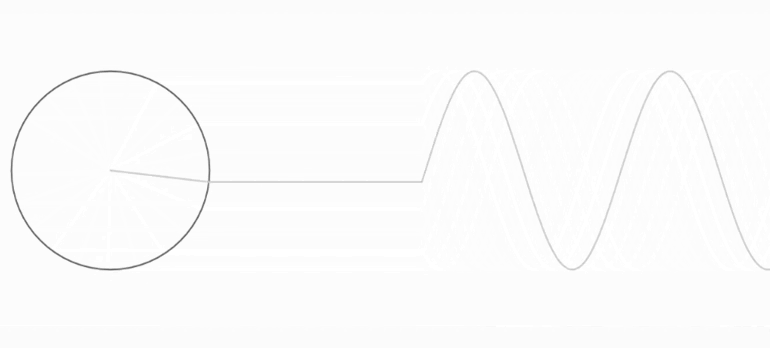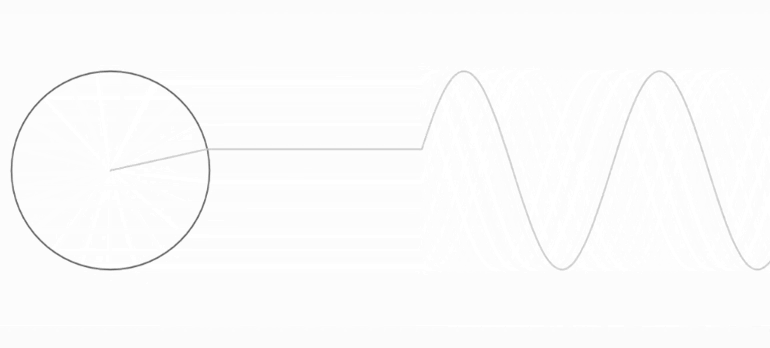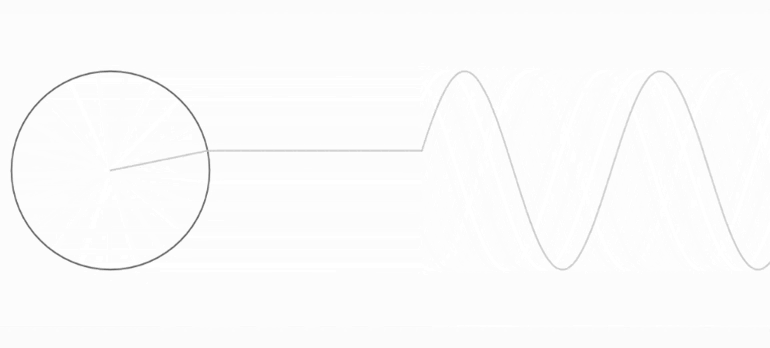
Fourier ens diu que podem escriure qualsevol funció periòdica, com la de dents de serra, únicament sumant sinus!

Només sumant aquestes funcions tant senzilles podem obtenir-ne qualsevol altra???

Sí! És fortíssim, trobant els coeficients adequats pels quals hem de multiplicar les nostres funcions trigonomètriques podrem obtenir una sèrie que igualarà a la nostra funció. Per exemple: la sèrie de Fourier de la funció de dents de serra és aquesta:

(1)   \begin{multline*} Sf(x) = \frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} \sin(nx) = \\ = \sin(x) -\frac{1}{2} \sin(2x) + \frac{1}{3} \sin(3x) - \cdots\end{multline*}

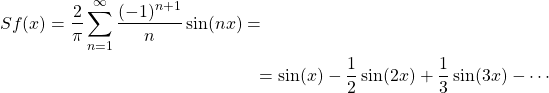
Però, què vol dir que sumant aquests infinits sinus tenim una funció igual a la de les dents de serra? Ja vam parlar de què volia dir tenir una suma infinita. Vam veure que, a mesura que anàvem afegint termes, la suma s’anava acostant més i més al punt; és a dir, tendia a aquell punt. En aquest cas, és exactament el mateix però per a cada punt concret, per a cada x. 

Estem fent una mica de trampes! Com pot ser que sumant funcions com el sinus, que són contínues ー les podem dibuixar sense aixecar el llapisー, siguin iguals a una que té tot de salts, com és el cas de la serra? Fourier ens diu que en els salts cal especificar una mica millor què vol dir aquest igual, però a tota la resta, si suméssim infinits termes, recuperaríem la funció de serra. 

Ho podem veure a l’animació següent. Aquí, movent la barra lliscant anem augmentant la quantitat de sinus que sumem. Veureu com a més termes, més s’assembla el dibuix que obtenim a les dents de serra.

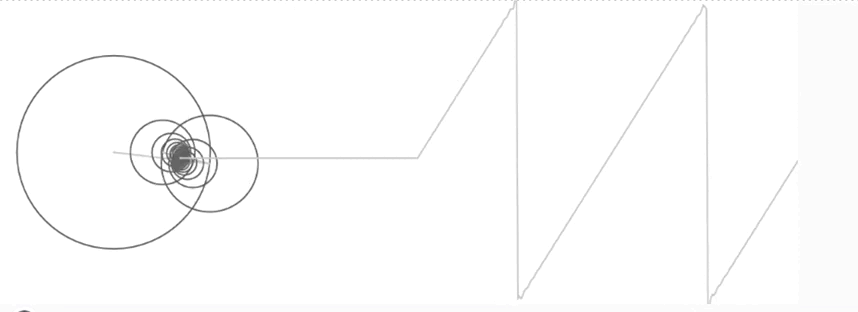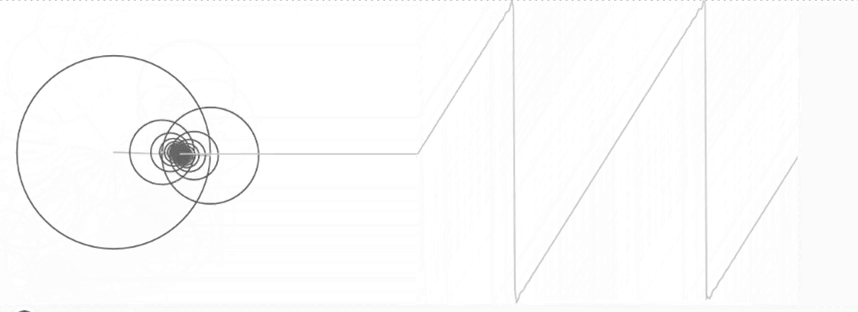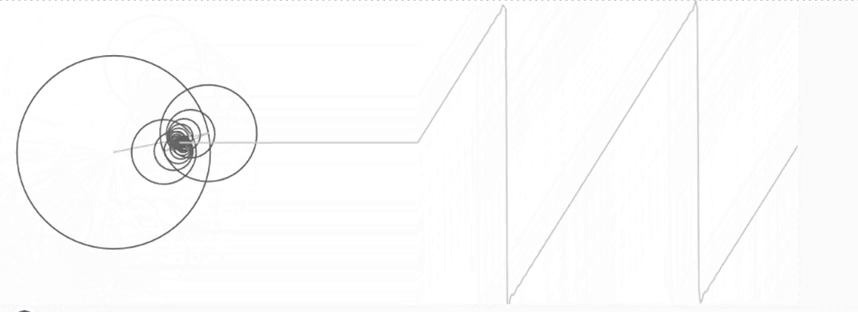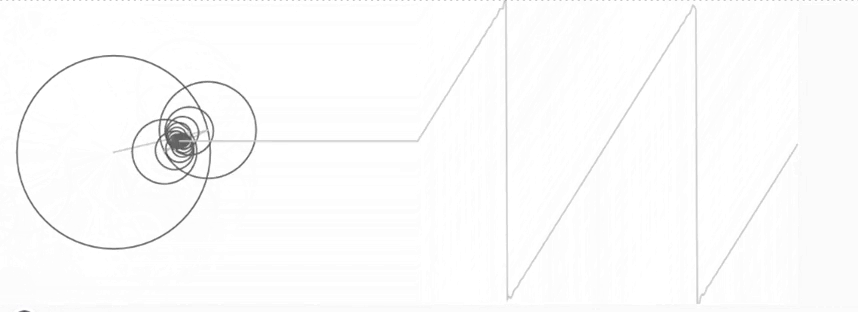
Per a poder jugar amb l’animació, podeu anar aquí.

Amb això, ja podem resoldre el problema de la barra calenta!

I els rellotges, i el dibuix?

Fourier va anar més enllà i va portar el seu estudi a dues dimensions. La fórmula per aquest cas és la següent. No us espanteu!

(2)   \begin{multline*} f(x) = \sum_{n=-\infty}^{\infty} c_n e^{ i n x} =\\= \cdots + c_{-2} e^{i (-2) x} + c_{-1} e^{i (-1) x} + c_{0} e^{i 0 x} + c_{1} e^{i 1 x} + c_{2} e^{ i 2 x} + \cdots \end{multline*}

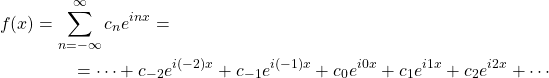
on,

    \[c_n = \int_{-\pi}^{\pi} f(x) e^{i n x}dx\]

No pretenem entrar en detall a on surt cada expressió d’aquestes equacions. Això no obstant, el resultat, tot i semblar un galimatíes, és d’una senzillesa espectacular. Si voleu saber per què, us recomanem el primer “Per saber-ne més” ーque té un nivell de detall més alt.

Però, què té a veure tot això amb els rellotges que dèiem al principi? La funció exponencial complexa e^{i x} fa una volta completa en un cercle de radi 1 quan x es mou entre 0 i 2\pi. Ho fa en el pla complex, però no ens hem de preocupar per això: podem entendre el pla complex com un pla normal de dues dimensions.

Si en vols saber més del pla complex i la relació amb els sinus i cosinus

L’arrel d’un nombre imaginari era il·legal a les matemàtiques fins fa relativament poc. En un moment determinat es va decidir donar nom a l’arrel de menys 1 i dir-li nombre imaginari o i, en contraposició als nombres reals que existien fins llavors.

Així, es van descobrir els nombres complexos, que tenen una part real i una imaginària. Si entenem un nombre real com un punt a una recta infinita, podem entendre un nombre complex com un punt a un pla: el pla complex. Així, la part real es correspon a l’eix horitzontal i la part imaginaria a l’eix real. Per exemple, el punt 3+2i seria el punt que està a tres unitats a la dreta de l’origen i dues amunt.

Però quina relació hi ha entre l’exponencial complexa i els sinus i els cosinus que trobàvem al món real? Doncs la seva relació ve donada pel que diuen que és una de les expressions més boniques de les matemàtiques:

</span><span style="font-weight: 400">e^{ix} = cos(x)+i sin(x) </span><span style="font-weight: 400">

Si us hi fixeu, relaciona el punt del cercle de radi 1 en el qual estem amb l’exponencial!

Si multipliquem l’exponencial per un 2 a l’exponent, farà la volta el doble de ràpid; si el multipliquem per un nombre negatiu, farà la volta al revés:

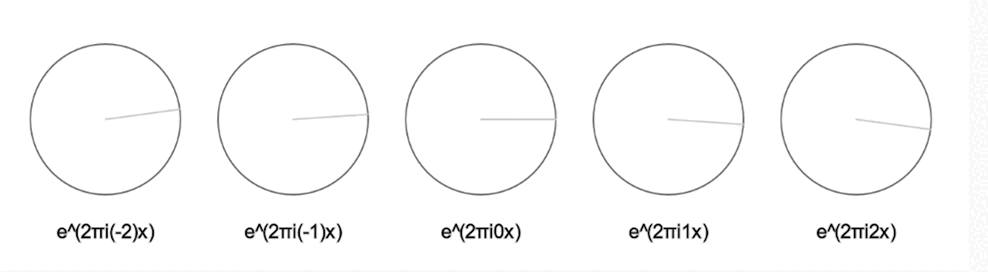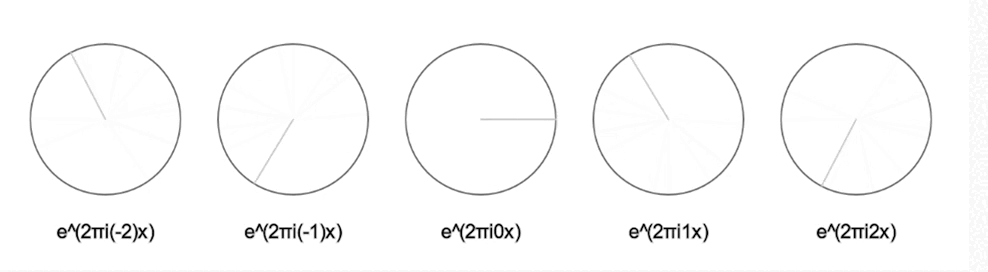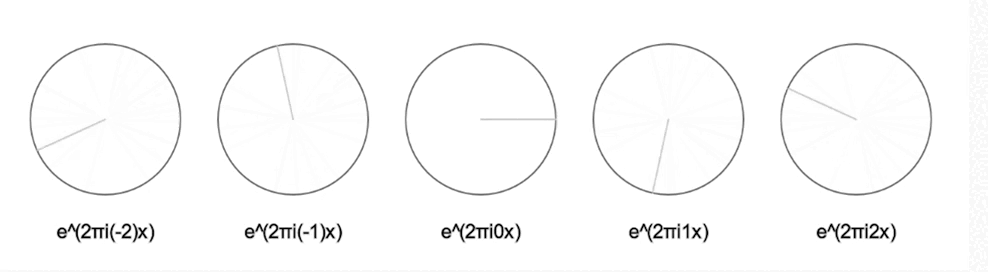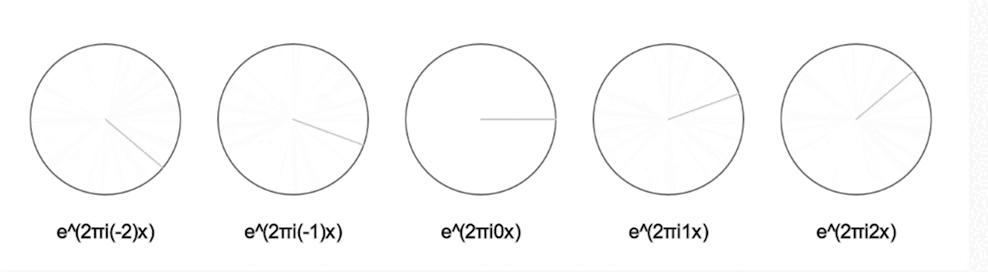
L’expressió de Fourier ens diu que únicament sumant infinits d’aquests rellotges ーajustant-ne la midaー podem resseguir qualsevol dibuix tancat!

Ja per acabar…

Hem vist que combinant tots aquests infinits rellotges que giren a una velocitat constant, modificant la seva grandària mitjançant els valors de les c_n, podem descriure qualsevol dibuix que vulguem. I aquí en teniu la prova. Amb la barra controlem el nombre de “rellotges” que afegim, segons Fourier, si en posem infinits, podrem recuperar exactament el dibuix. Evidentment, l’ordinador no pot treballar amb infinits rellotges, però tot i així podem obtenir una molt bona aproximació:

Malauradament, no podem inscerir per ara l’animació. Això no obstant, podeu entrar aquí si voleu fer els vostres dibuixos amb Fourier de la mateixa forma que nosaltres hem fet la C de Ciència Oberta al principi del reportatge.

Per saber-ne més

3blue1brown – But what is a Fourier series?

Viquipèdia – Funció trigonomètric

MathWorld – Fourier Series

Fonts:

  1. Extreta de la Viquipèdia sota domini CC amb atribució a Dnu72.
  2. Extreta de la Viquipèdia sota domini públic.

Les animacions són fetes des de Ciència Oberta basades en les de Coding Train i Olgaritme.