Predir el futur és una activitat molt útil per als humans, ja sigui per saber com evolucionarà l’economia o si un cometa acabarà xocant contra la Terra. Per això, els matemàtics porten estudiant des de fa temps models que descriuen com evolucionen els sistemes.
Podem predir amb exactitud com evolucionaran els sistemes? O hi ha casos en què mai no sabrem si s’arriba a un punt estable o a una destrucció completa d’aquests? La resposta potser la tenen uns petits rosegadors de l’àrtic:
Els lèmmings
Els lèmmings són uns petits rosegadors que habiten a les tundres i praderies àrtiques del nord del planeta. Estudiant la seva població es va descobrir que cada quatre anys desapareixien quasi per complet.
Això va portar a la teoria que, cada cert temps, aquests petits mamífers se suïcidaven col·lectivament llançant-se al mar des de dalt d’un penya-segat i ofegant-se, creant fascinació entre la societat i diverses històries i mites que encara perduren.

La prova del suïcidi
Disney, que a mitjans del segle passat feia alguns documentals de natura, va gravar suposadament aquest fet l’any 1958, en unes imatges que tothom en algun moment o altre ha vist:
Això no obstant, uns anys després, el càmera que va gravar aquestes imatges va confessar: hi havia un membre de la producció que agafava els lèmmings, els col·locava sobre una cinta giratòria posada just al costat del penya-segat i els disparava al buit, un horror.
Per tant, sembla que continuem sense tenir una explicació de per què cada quatre anys desapareix bona part de la població d’aquests animals. Un model matemàtic senzill ens pot donar una pista.
Les matemàtiques són les que maten els lèmmings
Intentem fer un model molt senzill per descriure com es comportarà la població dels lèmmings al llarg del temps. Suposem que a cada nova generació hi ha el doble d’individus que a l’anterior. Si en teníem n, a la generació següent n’hi ha 2n. Però no tots sobreviuran. Posem que, per a cada nova generació, calculem els que moriran multiplicant els de la generació anterior pels de la següent i dividint-ho entre 10. És a dir, n·2n/10.
Ho farem tot amb números petits perquè sigui més fàcil, però podeu pensar que són milers. D’aquesta forma, si tenim 2 lèmmings a la primera generació, a la segona n’hi haurà el doble: 4, però no en sobreviuran 2·4/10, és a dir, aproximadament un morirà. Així a la segona generació en tindrem 4-1=3. Fem el mateix per calcular la resta de generacions, ho veiem a la taula següent,
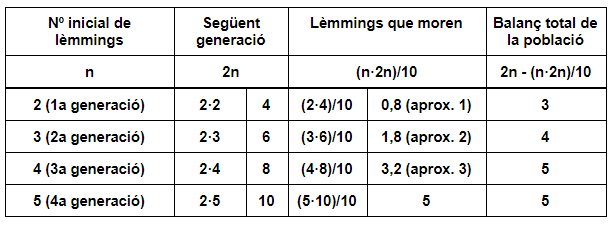
Aquí passa una cosa curiosa, la següent generació tornarà a tenir 5 lèmmings, i l’altra, i totes a partir d’ara. Hem arribat a un equilibri. A la figura següent podem veure aquest comportament. En aquest cas, ho hem normalitzat, és a dir, hem expressat el resultat com a tant per cent de lèmmings. Podem suposar que és el tant per cent respecte un nombre màxim total indefinit (així fem un model més general i ens estalviem saber el nombre de lèmmings exacte).
Però això no és el que passa als lèmmings
Podem jugar amb el nostre model per intentar que s’assembli més a allò que observem dels lèmmings. Ara, però, suposem que els lèmmings són més fèrtils i en lloc de duplicar-se, es multipliquen per 3,5 a cada nova generació. Si fem els càlculs suposant la mateixa equació per als que no sobreviuen, el comportament que observem és:
On veiem que la població oscil·la entre 4 valors, un dels quals és molt baix. Això és realment el que els passa als lèmmings. Podríem afinar més el model afegint les condicions climatològiques o combinant-lo amb models d’aliment i depredadors – tot això ho hem inclòs a la part dels lèmmings que no sobreviuen -, però amb aquest model tan senzill ja som capaços d’explicar per què cada quatre anys els lèmmings quasi desapareixen.
Podem mirar què passa si suposem que encara són més fèrtils i que cada nova generació es quadrupliquen. L’evolució que obtenim en aquest cas és:
Veiem que no sembla que se segueixi cap patró evident. A part, també passa una cosa diferent dels models d’abans. Al primer cas, per exemple, si posem un nombre de lèmmings inicial diferent, al cap d’unes quantes generacions arribarem al mateix punt estable. En canvi, en aquest veiem que això no passa, que posant només un lèmming més a l’inici tenim una evolució completament diferent.
Quan l’evolució d’un sistema en el temps varia molt en funció de les condicions inicials -com el cas en què es quadrupliquen- es diu que és un sistema caòtic.
El pèndol doble: el sistema caòtic per excel·lència
Mentre que el pèndol normal és un sistema que es comporta de forma tan estable que l’usem per mesurar el temps, quan en posem dos d’enganxats – construint un pèndol doble -, obtenim un sistema que es comporta de forma caòtica, és a dir, que té molta sensibilitat a les condicions inicials.
Podem tirar un pèndol doble dues vegades des de la “mateixa” posició que farà un recorregut completament diferent -ja que mai no serem capaços de tirar-lo exactament des del mateix punt.
En aquesta simulació podem veure com posant una diferència de 1/1000000 en les condicions inicials -una exactitud que a la pràctica mai no podríem aconseguir- al cap de poca estona cada pèndol doble fa un recorregut completament diferent.
És important fixar-se que no hi ha un component d’atzar -com passava al món quàntic en la superposició. En aquest cas, la posició del pèndol en cada instant de temps està clarament determinada per una equació que podem resoldre – de fet, aquesta simulació s’ha fet així -. El problema és que aquesta solució varia moltíssim quan posem un punt inicial o un altre -encara que aquests siguin molt propers!
En els sistemes que no són caòtics – com un pèndol normal – això no passa: si tenim dos punts inicials diferents però prou propers, el sistema es comportarà una mica diferent al principi, però al cap d’un temps acabarà evolucionant anàlogament. Per això, al final, el pèndol d’un rellotge acaba mesurant bé els segons independentment de la posició en què el deixem anar.
El descobridor del caos
Va ser el matemàtic francès Henri Poincaré qui va descobrir per primer cop un sistema caòtic i va decidir estudiar-ne les propietats. Estava estudiant si el sistema solar era un sistema estable o si, passat prou temps, els planetes sortirien de l’òrbita i acabarien xocant contra el sol o viatjant per l’espai.
Va descobrir que no es podia saber, ja que es tracta d’un sistema caòtic i només canviant molt poc la posició d’un planeta, canvia totalment el resultat. Sempre hi ha un límit de precisió en la mesura de la posició dels planetes – igual que amb un regle no es poden mesurar posicions amb més precisió que un mil·límetre – i per tant mai podrem decidir si el sistema solar és estable o no. Però, en qualsevol cas, a l’inici sabem com es comportarà – igual que podem predir que al principi el pèndol doble cauria avall – i, com que estem parlant a escala planetària, encara falta molt temps perquè ens haguem de preocupar.
Ja per acabar…
Trobem sistemes caòtics a quasi tots els racons de la natura. Un dels més típics és la meteorologia. Per fer una previsió, s’agafen les dades recollides per les estacions meteorològiques i se’n fan molts models diferents modificant-les una mica a cadascun. Al principi, la majoria de models coincideixen i per això les previsions a un o dos dies són més encertades. En canvi, al cap de 10 dies, un model pot dir que farà un sol radiant mentre que un altre, en el qual només s’ha canviat la temperatura en mig grau d’una estació, diu que plourà a bots i barrals. Per això, les previsions concretes a molts dies no tenen gaire sentit.
Convé recordar que estem parlant de meteorologia i previsions concretes per una regió i dia. Quan s’estudia l’evolució del clima, és a dir, l’evolució més general, com per exemple temperatures mitjanes, aleshores els models no són caòtics. Una mentida habitual dels negacionistes del canvi climàtic és dir que la meteorologia és un sistema caòtic i per això el canvi climàtic no es pot predir. Això no només no és cert, sinó que el canvi climàtic ja no tan sols el predim, sinó que el patim.
És per aquest motiu, que el fenomen del caos normalment s’explica amb la metàfora de l’efecte papallona. Canviar de forma molt petita les condicions inicials, és a dir, considerar el petit vent creat per una papallona, pot fer, al cap de prou dies, que tinguem un dia assolellat o un huracà!
Per saber-ne més
Nature – Why cycling lemming crash
Derivando – ¡Que viva el caos! | El sistema caótico más famoso
Marcus du Sautoy (TEDx Talks) – What will happen next?