Alguna vegada tots hem sentit a dir que, si viatgéssim molt de pressa, el temps passaria més a poc a poc. També hem sentit a parlar dels dos bessons, on un dels quals fa un viatge espacial a grans velocitats per descobrir en tornar que ha envellit menys que el seu germà. Tots aquests efectes els trobem descrits a la teoria de la relativitat especial.
La Teoria de la Relativitat Especial (publicada l’any 1905) és la culminació per part d’Einstein de la feina de molts altres, com els descobriments de Maxwell, Poincaré, Lorentz, etc. Al final la unió entre la teoria de la relativitat especial i la de la gravitació de Newton van concloure en la creació de la relativitat general d’Einstein.

La velocitat de la llum és invariant
Primer de tot, com podem mesurar la velocitat de la llum? Jo sempre hi he de pensar una estona. Realment, no sembla que la llum pugui tenir velocitat: quan pitgem l’interruptor el llum s’encén instantàniament. Però l’electricitat triga un temps a viatjar des de l’interruptor fins a l’aparell i, la llum generada, un temps més fins als nostres ulls. L’únic problema és que aquest temps és tan petit que ni ens n’adonem. De fet, pel nostre cos, la informació viatja de forma una mica més lenta que la llum. Així, quan al nostre cervell arriba la confirmació que hem sigut capaços de prémer amb èxit el botó, ja fa estona que el llum s’ha encès.
Així doncs, per mesurar-la, cal calcular quant temps triga a recórrer una determinada distància o quant triga a il·luminar dues superfícies separades, però haurà de ser prou gran per poder-nos-en adonar.
La velocitat de la llum sempre és la mateixa
Tots hem sentit a dir que la velocitat de la llum és invariant, independentment de la velocitat en què ens movem respecte a l’emissor. És la típica pregunta del trivial que ja no fallaríem. Fins i tot tenim la cançó d’en Joan Miquel Oliver que ens ho recorda. Però és molt contra-intuïtiu si hi penses dos minuts. Imagina’t que mires un tren des de l’andana quan aquest va, per exemple, a 90 km/h i algú hi corre per dins endavant a 10 km/h. Nosaltres veurem que la persona es mou a 100 km/h respecte a l’andana -que és el nostre sistema de referència. En canvi, si el corredor anés en sentit contrari, a nosaltres igualment ens semblaria que avança endavant, però aquest cop a 80 km/h.
No hauria de passar el mateix amb la llum que surt dels fars del davant del tren? Si mesurem la velocitat de la llum dels fars des de l’andana, no hauria de ser 90 km/h més ràpida que la mesurada per algú dalt del tren (com passava amb el corredor)?
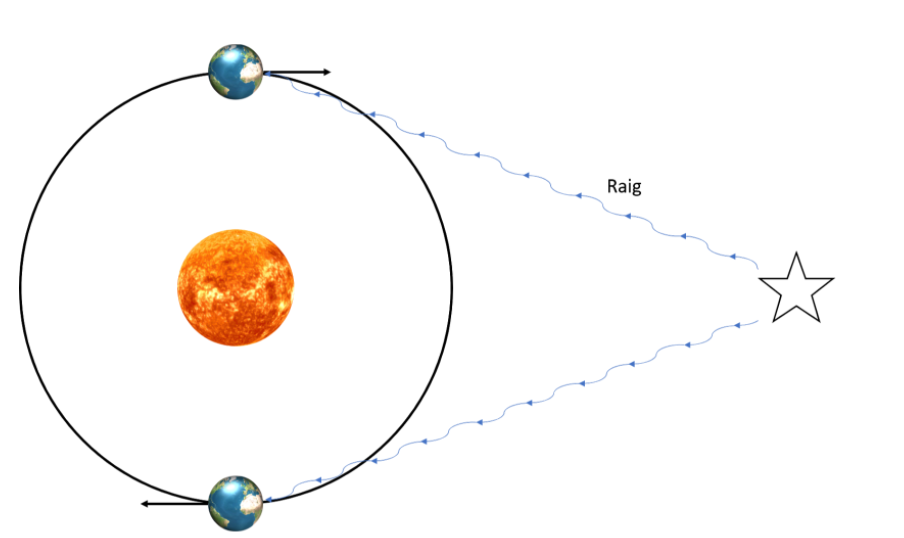
Uns científics van mesurar la velocitat de la llum que arribava d’una estrella a la primavera i a la tardor. En un cas, la Terra es movia cap a l’estrella i en l’altre s’allunyava. Esperaríem trobar que la velocitat que mesurem és diferent -com passava amb el tren-, però després de l’experiment van veure que en els dos casos la velocitat de la llum era la mateixa. Es podria pensar que aquest fet es donava per algun efecte estrany en viatjar per l’univers, però uns anys més endavant, amb un conjunt de miralls, Michelson va fer un estudi semblant a la Terra i va arribar a la mateixa conclusió sorprenent: la velocitat de la llum és la mateixa independentment del sistema de referència. És a dir, que per molt que el tren anés a altes velocitats, la llum emesa per les bombetes tindria la mateixa velocitat vista des de l’andana que l’emesa per una llanterna en aquesta.
El temps es dilata
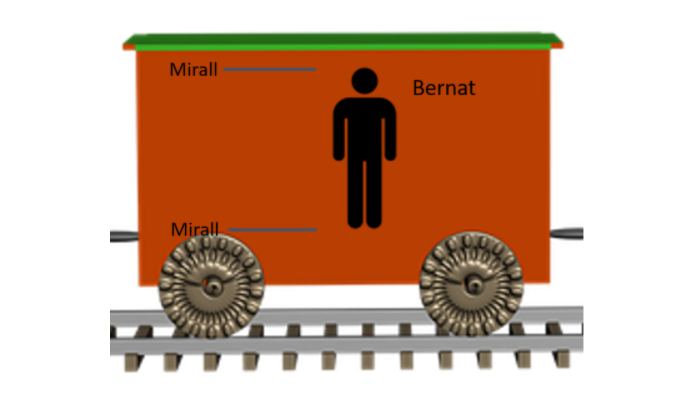
Imaginem que en Bernat és dalt d’un tren. En Bernat mesura el temps però ho fa amb un rellotge bastant particular. Consisteix de dos miralls posats de forma paral·lela col·locats perpendiculars a la direcció del tren.
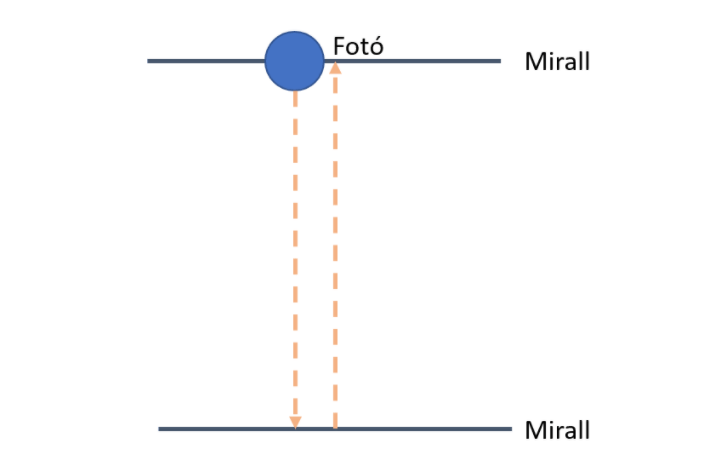
Enfoquem amb un làser des d’un dels miralls cap a l’altre, podem pensar que viatja un fotó de llum sol. Aquest es reflectirà en l’altre i el rebrem de nou al primer mirall. Podem imaginar el fotó de llum com una piloteta que rebota als miralls. Cada vegada que el feix retorni al mirall original, direm que ha passat un segon. Si us hi fixeu, el nostre rellotge és molt similar a un de pèndol.
L’Alba és a l’andana i també té un rellotge d’aquests tan especials. Els dos estan sincronitzats. Quan el tren està parat, l’Alba no té cap problema i veu que el rellotge d’en Bernat marca els segons igual que el seu.
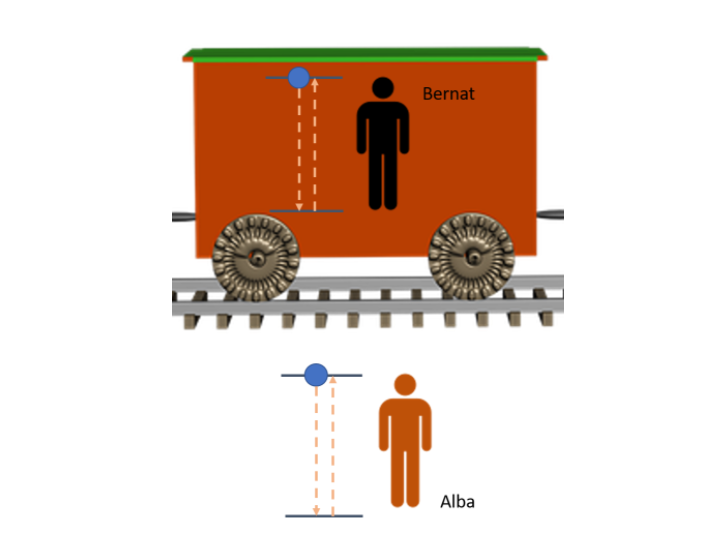
compta els segons igual que el del Bernat.
Ara però, el tren on va en Bernat passa per l’estació on és l’Alba a una velocitat molt alta. Ella continua comparant el seu rellotge amb el d’en Bernat. En aquest cas, el tren on és en Bernat es mou endavant. Per tant, per l’Alba, mentre el fotó del rellotge d’en Bernat viatja d’un mirall a l’altre, el tren s’haurà mogut i per tant el fotó haurà de desplaçar-se també endavant com el tren. És a dir, haurà de recórrer més distància.
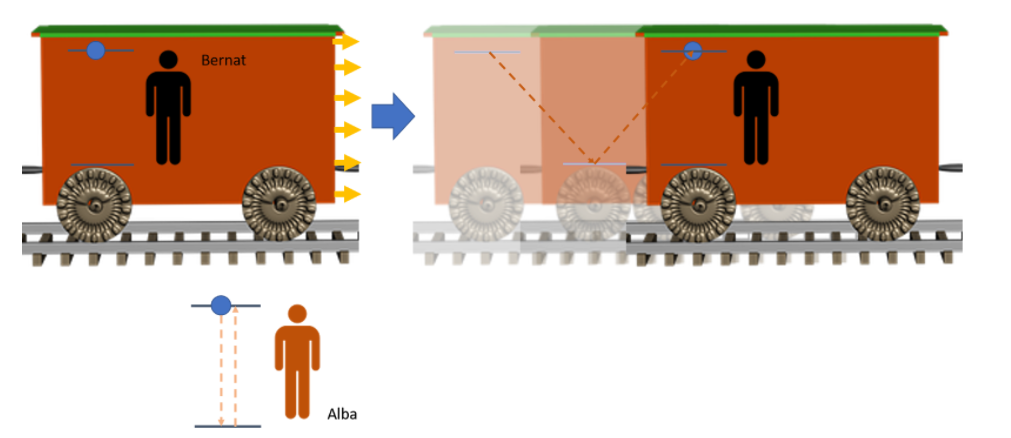
Si les velocitats se sumessin, no passaria res: per l’Alba la llum aniria més de pressa dalt del tren i el segon del rellotge del Bernat seria el mateix que el seu. Però la velocitat de la llum és invariant, és sempre la mateixa. Per tant l’Alba veu el fotó del Bernat movent-se a la mateixa velocitat que el seu! Com que aquest haurà de recórrer més distància, trigarà més. És a dir, quan l’Alba vegi que el rellotge del Bernat ha marcat un segon, el seu n’haurà marcat més.
Podem dir doncs que, quan en Bernat baixi del tren, per ell haurà passat menys temps que per l’Alba.
Ja per acabar…
Les conclusions de la relativitat espacial tal com l’hem vist és que espai i temps no són dues dimensions independents com ens semblava abans, sinó que estan profundament relacionades. Si continuéssim desenvolupant la teoria, descobriríem que en viatjar a grans velocitats l’espai s’escurça i que sumar velocitats no és tan fàcil com semblava. Tot i això, només en podem notar els efectes a grans velocitats; agafant un Rodalies, el temps no ens passarà pas més lent que al germà que s’ha quedat a casa!
Per saber-ne més
Date un Vlog – HOY SÍ que vas a entender la relatividad especial
QuantumFracture – ¿Qué es la relatividad especial de Einstein?
Eduard Massó i Soler – Curs de Relativitat Especial